Types of triangles

Types of triangles may be classified by their sides, by their angles or by a combination of both sides and angles.

Triangles classified by their sides:

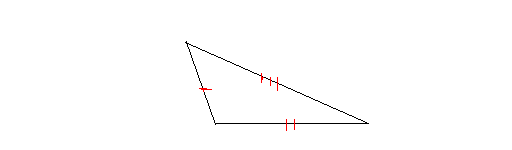
Scalene triangle: A scalene triangle is a triangle that has no equal sides. The following is a scalene triangle.

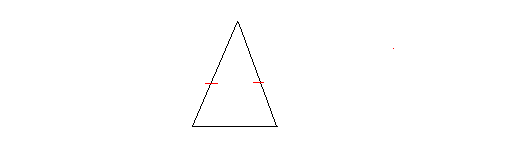
Isosceles triangle: An isosceles triangle is a triangle that has two equal sides. The following is an isosceles triangle.



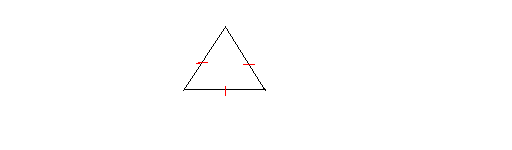
Equilateral triangle: An equilateral triangle is a triangle that has three equal sides. The following is an equilateral triangle.



Triangles classify by their angles:

Right triangle: A right triangle has a 90 degrees angle.The following is a right triangle.



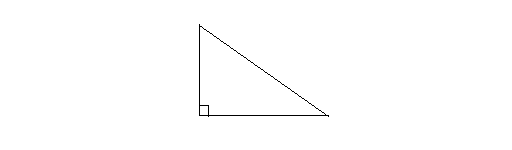
Obtuse triangle: An obtuse triangle has one angle that is bigger than 90 degrees (Obtuse angle). The following is an obtuse triangle.



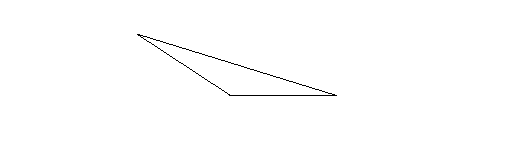
Acute triangle: In an acute triangle, all angle are less than 90 degrees, so all angles are acute angles.The following is an acute triangle.



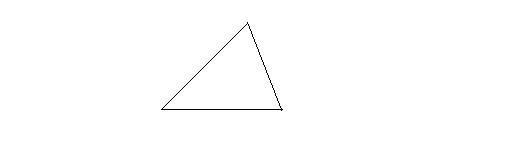
We can also name triangles using angles and sides at the same time.

If a triangle has one right angle and two equal sides, we can call that triangle right isosceles triangle.

If a triangle has only acute angles and no equal sides, we can call that triangle acute scalene triangle.

If a triangle has two equal sides and one obtuse angle, we can call that triangle obtuse isosceles triangle.

Notice that an angle cannot be obtuse and equilateral at the same time. An equilateral triangle cannot have an obtuse angle because all 3 angles in an equilateral triangle measure 60 degrees.

Pythagorus

Anglo Urdu Boys' High School

History of mathematics

Greek mathematician Pythagoras (c. 570 – c. 495 BC), commonly credited with discovering the Pythagorean theorem

The evolution of mathematics might be seen as an ever-increasing series of abstractions, or alternatively an expansion of subject matter. The first abstraction, which is shared by many animals,^[19] was probably that of numbers: the realization that a collection of two apples and a collection of two oranges (for example) have something in common, namely quantity of their members.

Mayan numerals

Evidenced by tallies found on bone, in addition to recognizing how to count physical objects, prehistoric peoples may have also recognized how to count abstract quantities, like time – days, seasons, years.^[20]
More complex mathematics did not appear until around 3000 BC, when the Babylonians and Egyptians began using arithmetic, algebra and geometry for taxation and other financial calculations, for building and construction, and for astronomy.^[21] The earliest uses of mathematics were in trading, land measurement, painting and weaving patterns and the recording of time.
In Babylonian mathematics elementary arithmetic (addition, subtraction, multiplication and division) first appears in the archaeological record. Numeracy pre-dated writing and numeral systems have been many and diverse, with the first known written numerals created by Egyptians in Middle Kingdom texts such as the Rhind Mathematical Papyrus.^{[citation needed]}
Between 600 and 300 BC the Ancient Greeks began a systematic study of mathematics in its own right with Greek mathematics.
Mathematics has since been greatly extended, and there has been a fruitful interaction between mathematics and science, to the benefit of both. Mathematical discoveries continue to be made today. According to Mikhail B. Sevryuk, in the January 2006 issue of the Bulletin of the American Mathematical Society, "The number of papers and books included in the Mathematical Reviews database since 1940 (the first year of operation of MR) is now more than 1.9 million, and more than 75 thousand items are added to the database each year. The overwhelming majority of works in this ocean contain new mathematical theorems and their proofs